statistiques
Temps de lecture :Le symbole (–) placé au-dessus d’une expression en signifie la moyenne.
définitions
somme

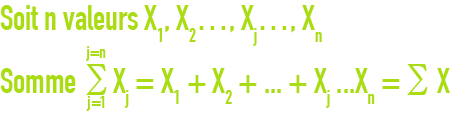
moyenne arithmétique

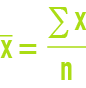
moyenne arithmétique pondérée

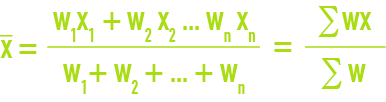
médiane
La médiane d’un ensemble de nombres rangés par ordre de grandeur croissante est la valeur du milieu, ou la moyenne arithmétique des deux valeurs centrales (cas d’un nombre pair de valeurs).
mode
Le mode d’un ensemble de nombres est le nombre que l’on rencontre le plus fréquemment, c’est-à-dire celui qui a la plus grande fréquence. Le mode peut ne pas exister ou ne pas être unique.
Relation empirique entre la moyenne, la médiane et le mode (figure 1) :

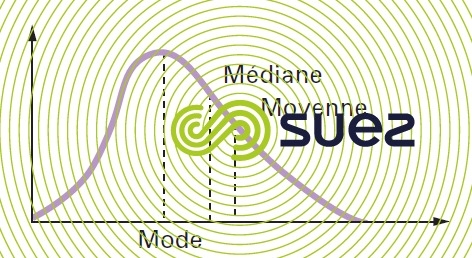

Pour des courbes de densité unimodale modérément asymétrique, on a la relation empirique suivante :


moyenne géométrique G :

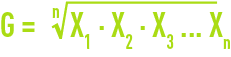
moyenne quadratique MQ :

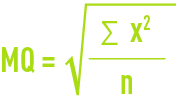
écart moyen EM :

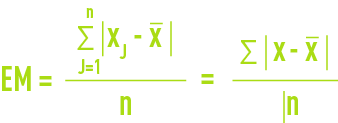
écart type s

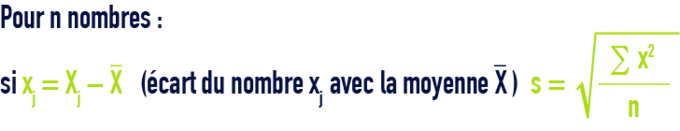
variance V

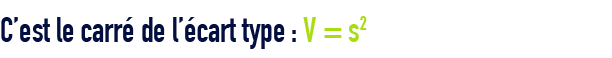
propriété de l’écart type
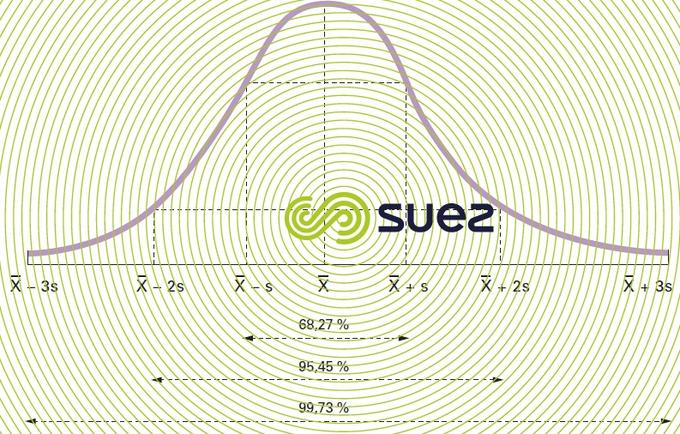
Pour une distribution normale, ou distribution de Laplace-Gauss (figure 2), il apparaît que :




méthode graphique d’ajustement d’une courbe
À partir d’un diagramme de dispersion (figure 3), on peut souvent représenter une courbe continue approchant les données. Une telle courbe est appelée courbe d’ajustement.



La méthode la plus classique est celle des moindres carrés.
définition
Parmi toutes les courbes qui approchent un ensemble de données, celle qui donne le meilleur ajustement est celle qui vérifie la propriété suivante :

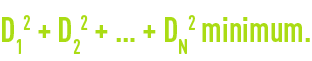
D1, D2, DN étant les distances entre courbe et points expérimentaux (figure 4).



On l’appelle la courbe des moindres carrés.
droite de régression des moindres carrées

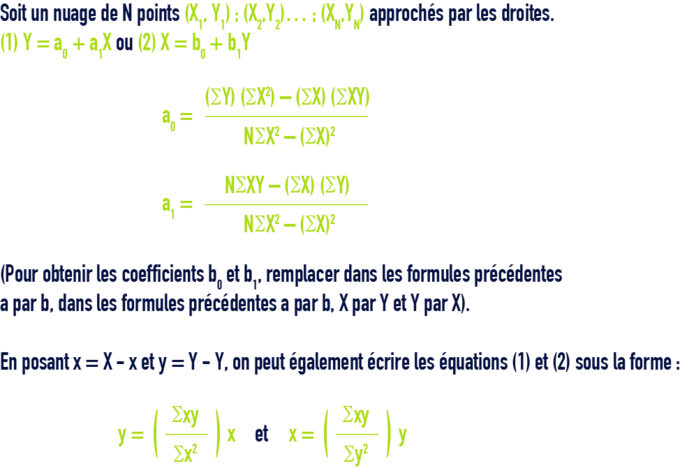
Outil Marque-page
Cliquez sur l'outil marque-page, puis surlignez le dernier paragraphe lu pour pouvoir poursuivre ultérieurement votre lecture.












