équations de base

filtration en profondeur

perte de charge

Au cours de sa percolation au travers d’un lit filtrant granulaire, l’eau subit par frottement une perte d’éner­gie, c’est-à-dire de pression, appelée perte de charge. Celle-ci est régie à faible vitesse (écoulement en régime laminaire) par la loi de Darcy :

où V : vitesse de filtration,
K : perméabilité de la couche filtrante,
ΔP : perte de charge à travers la couche filtrante,
H : hauteur de couche considérée,
μ : viscosité dynamique de l’eau,
R : résistance à la filtration de la couche filtrante.

La perte de charge ΔP est proportionnelle à la vitesse de filtration V, à la viscosité dynamique de l’eau, à la hauteur de couche et inversement proportionnelle à la perméabilité du milieu filtrant (ou directement pro­portionnelle à la résistance de ce milieu).

La formule de Kozeny (ou Kozeny-Carman) précise celle de Darcy en faisant apparaître l’influence de la porosité du milieu filtrant et de la surface spécifique des grains :

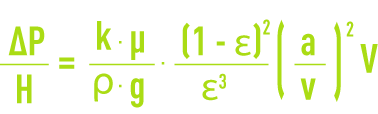
avec en plus des définitions ci-dessus :
k : constante de Kozeny (environ 5),
ρ : masse volumique du fluide,
g : accélération de la pesanteur,
ε : porosité du milieu filtrant,
a/v : surface spécifique par unité de volume des grains filtrants de diamètre d, soit 6/d pour un grain sphé­rique.

Pour de plus fortes vitesses, en courant descendant ou ascendant (par exemple lavage ou approche de la fluidisation), on passe en régime transitoire ou turbulent. On doit alors appliquer la formule d’Ergun, dérivée de celle de Kozeny en modifiant k et en lui ajoutant un terme correctif représentatif de la perte d’énergie ciné­tique dans le milieu :

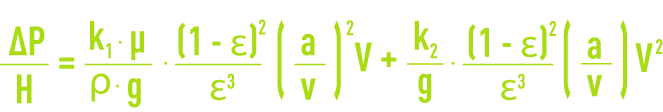
avec k₁ = 4,17,
k₂ = 0,3 (grains ronds) à 0,48 (grains concassés).

La formule d’Ergun est plus générale, car elle s’applique à tous les régimes hydrauliques. Pour les fortes vitesses, le second terme, proportionnel au carré de la vitesse, devient prépondérant.

Des corrélations empiriques ont été établies. Par exemple la corrélation ci-dessous est valable pour du sable à grains ronds dans la plage granulomètrique 0,5 à 1,5 mm :

où TE : taille effective du sable (voir caractéristiques des matériaux),
μ_t : viscosité dynamique de l’eau à t °C.

L’exposant 1,20 affectant la vitesse traduit le fait que l’écoulement n’est plus parfaitement laminaire aux vitesses usuelles.

influence du colmatage

Les formules ci-dessus s’appliquent à un milieu filtrant homogène et propre (R constant sur toute la hau­teur). Or, au fur et à mesure qu’un liquide contenant des MES percole à travers ce milieu, la capture progres­sive de ces MES influe sur les caractéristiques du milieu, en particulier sa porosité qui décroît et la perte de charge qui croît suivant une loi empirique du type :

avec σ : dépôt spécifique (volume de dépôt par unité de volume de lit filtrant),
a : coefficient expérimental.

La répartition du colmatage dans un filtre est hétérogène (les couches supérieures retenant plus de parti­cules) et les différents coefficients peuvent prendre des valeurs très différentes en fonction de la nature des solides à retenir et suivant qu’ils sont coagulés ou non. Il reste donc indispensable de passer par l’expéri­mentation, les lois ci-dessus permettant ensuite d’interpoler ou d’extrapoler les résultats constatés.

vitesse minimale de fluidisation

En courant ascendant on peut écrire que la vitesse minimale de fluidisation (V_mf) est atteinte lorsque la perte de charge est égale au poids apparent du lit par unité de surface (poids réel moins poussée d’Archimède) :

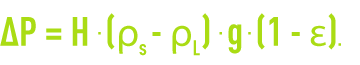
Il existe par ailleurs des équations empiriques (Leva, Moll) permettant de calculer cette vitesse. Le tableau 37 (dans fluidisation) donne des valeurs de V_mf pour des matériaux usuels.

filtration d’un liquide chargé avec formation d’un gâteau

On considère ici la filtration sur support d’un liquide boueux avec formation d’un gâteau d’épaisseur crois­sante. Ceci est le cas du traitement des boues (filtration de boue sous pression en filtre-presse ou filtre à bande presseuse).

Dans l’expression de la loi de Darcy, on admet alors que R comprend deux résistances en série, d’une part la résistance R_g du gâteau et d’autre part, la résistance initiale R_m de la toile filtrante.

La mise en équation est développée à la section les filtres. Voir également le test de filtrabilité pour les pro­tocoles d’essai en laboratoire permettant la mesure de R et du coefficient de compressibilité.

On peut utiliser une approche similaire pour les systèmes de filtration sur toile ou cartouche filtrante.